问题
单项选择题
设A，B，C是n阶矩阵，并满足ABAC=E，则下列结论中不正确的是
A．ATBTATCT=E.
B．BAC=CAB.
C．BA2C=E.
D．ACAB=CABA.
答案
参考答案：C
解析：这一类题目要注意的是矩阵乘法没有交换律、有零因子、没有消去律等法则，由ABAC=E知矩阵A，B，C均可逆，那么由
ABAC=E
ABA=C-1
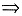CABA=E.
从而(CABA)T=ET，即ATBTATCT=E，故A正确.
由ABAC=E知A-1=BAC，由CABA=E知A-1=CAB，从而BAC=CAB，故B正确.
由ABAC=E
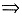CABA=E
ACAB=E，故D正确，
由排除法可知，C不正确，故选C.
