问题
问答题
设
(Ⅰ)求
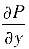与
(Ⅱ)求
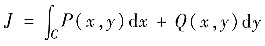，其中C是圆周x2+y2=32，取逆时针方向.
答案
参考答案：(Ⅰ)
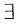
(Ⅱ)因为
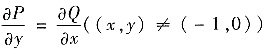
可考虑用格林公式计算J. 因为P，Q在点(-1，0)处没定义，所以不能在C围成的区域D上直接用格林公式. 但可在D中挖掉以(-1，0)为圆心，ε＞0充分小为半径的圆所余下的区域中用格林公式见下图，求解如下：
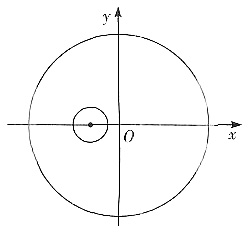
以(-1，0)为圆心ε＞0充分小为半径作圆周
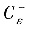(取顺时针方向)，Cε与C围成的区域记为Dε，在Dε上用格林公式得
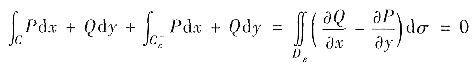
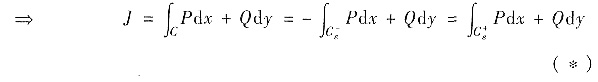
其中
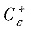取逆时针方向，
用“控洞法”求得(*)式后，可用Cε的方程
(x+1)2+y2=ε2
简化被积表达式，然后用格林公式得
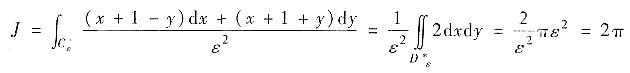
其中
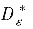是
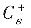所围的区域.
解析：①我们用
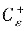的参数方程
x+1=εcost，y=εsint，t∈[0，2π]
来计算
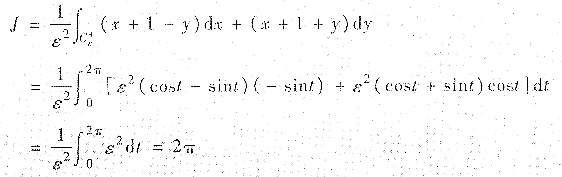
②本题有如下变式：
(Ⅲ)分别讨论在y＞0与x＜0且(x，y)≠(-1，0)时积分
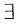是否与路径无关.
y＞0是单连通区域，且有
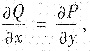因此y＞0中积分与路径无关.
区域D：x＜0，(x，y)≠(-1，0)不是单连通区域，此时还须求出某积分
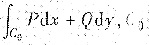是环绕(-1，0)的某闭曲线. 随(Ⅱ)中已求出
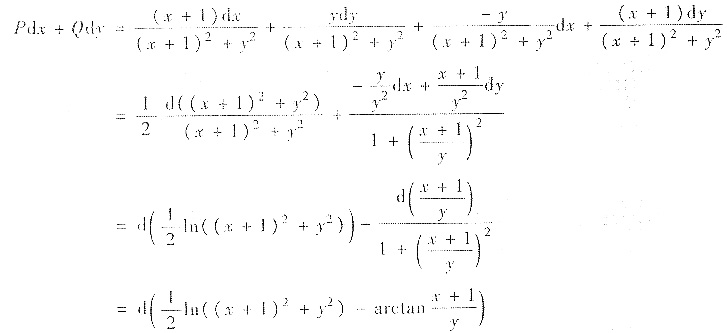
取
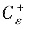使得
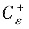包含在D中
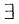一条闭曲线
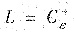使得
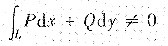
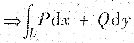在区域D：x＜0(x，y)≠(-1，0)内不是与路径无关的.
(Ⅳ)分别讨论y＞0与x＜0且(x，y)≠(-1，0)时Pdx+Qdy是否
原函数，若
并求出原函数.
注意P，Q在区域D连续时
Pdx+Qdy在D
原函数
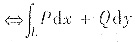在D与路径无关. y＞0是单连通区域，且有
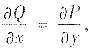因此y＞0中Pdx+Qdy
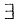原函数
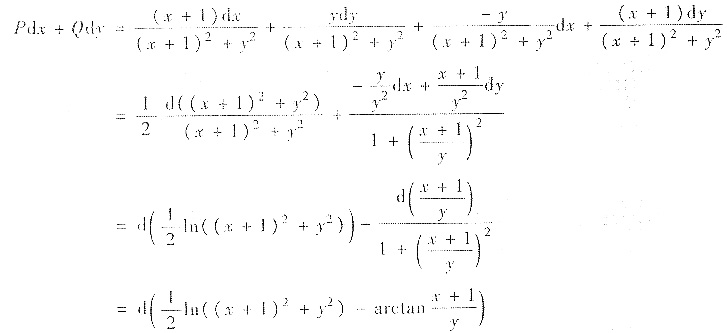
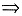Pdx+Qdy的原函数为
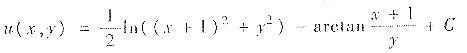
C为
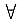常数.
x＜0且(x，y)≠(-1，0)时Pdx+Qdy不
原函数.