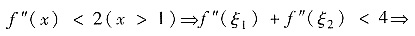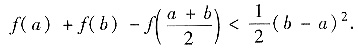问题
问答题
设1≤a<b,函数f(x)=xln2x,求证f(x)满足不等式
(Ⅰ)0<f″(x)<2(x>1).
(Ⅱ)
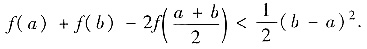
答案
参考答案:(Ⅰ)求出
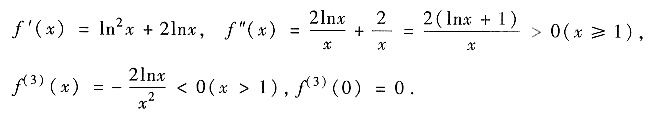
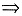 f″(x)在[1,+∞)单调下降
f″(x)在[1,+∞)单调下降
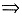 f″(x)<f″(1)=2(x>1).
f″(x)<f″(1)=2(x>1).
(Ⅱ)方法1°引进辅助函数利用单调性证明不等式. 将b改为x,考察辅助函数
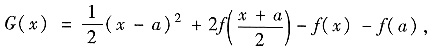
其中1≤a≤x≤b.
由
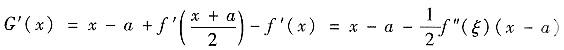
其中
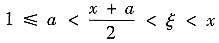 . 又当1≤a<x时f″(x)<2,于是当1≤a<x时
. 又当1≤a<x时f″(x)<2,于是当1≤a<x时
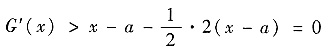
即G(x)在[a,+∞)↗,从而G(x)>G(a)=0(x>a),特别有G(b)>0,即
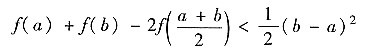
方法2°用泰勒公式,在
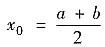 处展开,有
处展开,有
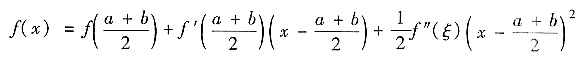
分别取被展开点x=a,b,得
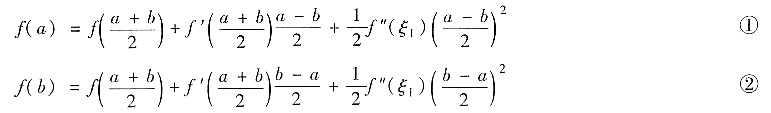
其中
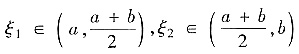
①+②得
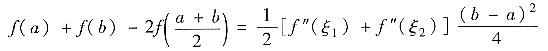
由题(Ⅰ),