设f(x)，g(x)在点x=x0处可导且f(x0)=g(x0)=0，f′(x0)g′(x0)＜0，则
A．x0不是f(x)g(x)的驻点.
B．x0是f(x)g(x)的驻点，但不是f(x)g(x)的极值点.
C．x0是f(x)g(x)的驻点，且是f(x)g(x)的极小值点.
D．x0是f(x)g(x)的驻点，且是f(x)g(x)的极大值点.
参考答案：D
解析：由于
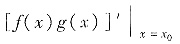=f′(x0)g(x0)+f(x0)g′(x0)=0，因此x=x0是f(x)g(x)的驻点，进一步考察是否是它的极值点.
由条件f′(x0)g′(x0)＜0
f′(x0)＜0，g′(x0)＞0(或f′(x0)＞0，g′(x0)＜0). 由
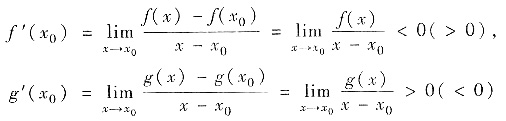
及极限的保号性质
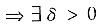，当x∈(x0-δ，x0 +δ)，x≠x0时
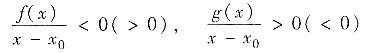
x∈(x0，x0+δ)时
f(x)＜0(＞0)，g(x)＞0(＜0)；
x∈(x0-δ，x0)时
f(x)＞0(＜0)，g(x)＜0(＞0)
x∈(x0-δ，x0+δ)，x≠x0时
f(x)g(x)＜0=f(x0)g(x0)
x=x0是f(x)g(x)的极大值点，因此选D.
①可特殊选取f(x)=x-x0，g(x)=-(x-x0)，则f(x)，g(x)满足题中条件，显然x=x0是f(x)g(x)=-(x-x0)2的驻点，且是其极大值点，即对此f(x)，g(x)，选项A.B，C不对，D成立. 因此选D.
②在题设下，已知
，但不能求f(x)g(x)的二阶导数(因为没假设f(x)，g(x)二阶可导). 若我们加强条件，设f(x)，g(x)在x=x0处二阶可导
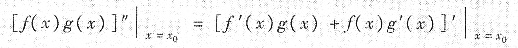
=f″(x0)g(x0)+2f′(x0)g′(x0)+f(x0)g″(x0)
=2f′(x0)g′(x0)＜0
x=x0是f(x)g(x)的极大值点. 因此，选D.