问题
问答题
已知
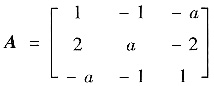 ,求A的特征值与特征向量,并指出A可以相似对角化的条件.
,求A的特征值与特征向量,并指出A可以相似对角化的条件.
答案
参考答案:由矩阵A的特征多项式
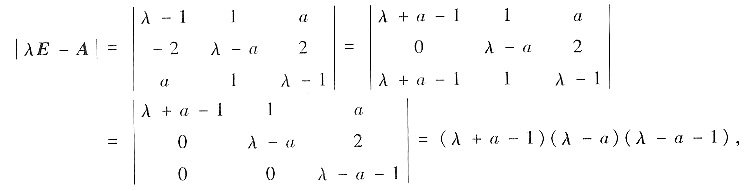
得到A的特征值是λ1=1-a,A2=a,λ3=a+1.
由[(1 -a)E-A]x=0,
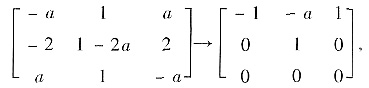
得到属于λ1=1-a的特征向量是α1=k1(1,0,1)T,k1≠0.
由(aE-A)x=0,
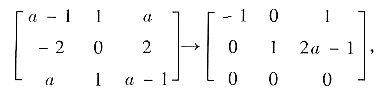
得到属于λ2=a的特征向量是α2=k2(1,1-2a,1)T,k2≠0.
由[(a+1)E-A]x=0,
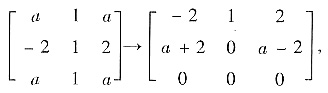
得到属于λ3=a+1的特征向量α3=k3(2-a,-4a,a+2)T,k3≠0.
如果λ1,λ2,λ3互不相同,即1-a≠a,1-a≠a+1,a≠a+1,即
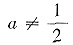 且a≠0,则矩阵A有3个不同的特征值,A可以相似对角化.
且a≠0,则矩阵A有3个不同的特征值,A可以相似对角化.
若
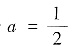 即
即
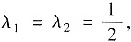 此时A只有一个线性无关的特征向量,故A不能相似对角化,
此时A只有一个线性无关的特征向量,故A不能相似对角化,
若a=0,即λ1=λ3=1,此时A只有一个线性无关的特征向量,故A不能相似对角化,
解析:不要错误地认为A必能对角化. 特征值含参数时,可能会有重根,因此要分析判断.当a≠0且
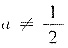 时,请写出可逆矩阵P及对角矩阵
时,请写出可逆矩阵P及对角矩阵
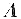 .
.

