问题
选择题
已知双曲线
|
答案
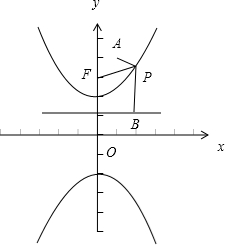
∵双曲线
-y2 16
=1的离心率e=x2 9
,5 4
∴
=|PF| |PB|
,即5 4
|PF|=|PB|,4 5
∴|PA|+
|PF|的值最小时的P点的坐标是过点A作准线的垂线与抛物线的上支的交点,4 5
∵A(1,6),∴设P(1,y),
把P(1,y)代入双曲线
-y2 16
=1,得x2 9
-y2 16
=1,解得y=±1 9
.4 10 3
∴P(1,
).4 10 3
故选A.
