问题
问答题
质量为m、半径为r的小球初始时刻静止放置于另一质量为M、半径为R的大球正上方，如图所示，两球心连线沿重力方向。由于该状态不是稳态，小球会从大球顶上滑落。忽略一切可能摩擦，求出以下两种极限情况下大球的最终速度：
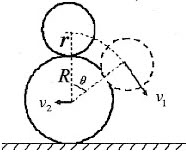
1．m＜＜M：2．m＞＞M。
答案
参考答案：
求解本题的关键之处是求出两球分离时小球球心的偏角，或者cosθ(记为x) 。
在分离的瞬间，两球间作用力为零，大球无加速度，小球加速度为g。x满足如下方程：
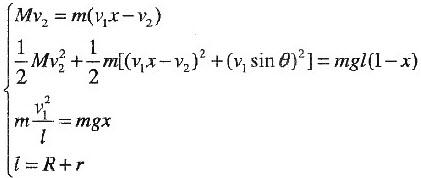
由此可知
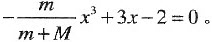所以，
1．当m＜＜M，3x-2=0，解得x=2/3；故v2=0；
2．当m＞＞M，
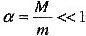，-x3+3x-2=0，解得x=1；故
