(1)求双曲线9x2-25y2=225的实轴长、虚轴长、焦点坐标、准线方程

问题问答题

(1)求双曲线9x²-25y²=225的实轴长、虚轴长、焦点坐标、准线方程、渐近线方程、离心率.
(2)设直线y=ax+b与双曲线3x²-y²=1交于A、B，以AB为直径的圆过原点，求点P(a，b)的轨迹方程．

答案

参考答案：

(1)将双曲线方程化为标准方程得

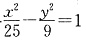
∴a=5，b=3，

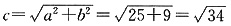
∴实轴长2a=10，虚轴长2b=6

焦点坐标

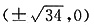，准线方程

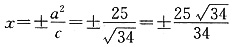
渐近线方程

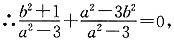
离心率

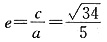
(2)联立y=ax+b和双曲线3x²-y²=1，得：

3x²-(ax+b)²=1，即(3-a²)x²-2abx-b²-1=0

设A、B坐标分别为(x₁，y₁)、(x₂，y₂)

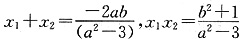
则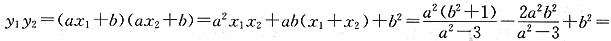

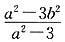
∵O在圆上，AB是直径，∴∠AOB=90°

∴OA· OB=0，即x₁x₂+y₁y₂=0

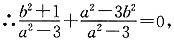解得：2b²-a²=1

即P的轨迹方程为2y²-x²=1