参考答案：

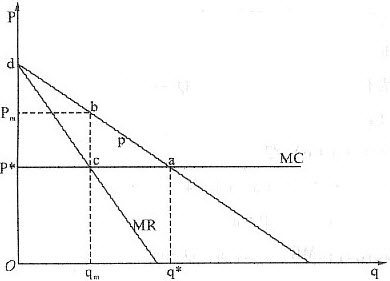
如图所示，垄断厂商是理性的，追求利润最大化，要满足MR=MC的条件。这时，垄断产量为q_m，垄断价格为P_m，利润为四边形P_mP^*cb的面积。

若完全竞争，厂商利润最大化，要满足MR=MC的条件，因为完全竞争厂商MR=AR=P，因此，完全竞争厂商P^*=MC，产量为q^*，利润为零。

显然，P_m＞P^*，q_m＜q^*。

垄断与完全竞争相比，产量更低，价格更高，通过低产量高价格获得垄断利润。

我们用总剩余来衡量效率，在完全竞争市场，P^*=MC，总剩余为dP^*a的面积，可以证明，完全竞争均衡时，是有效率的，即总剩余达到最大化。若P^*＞MC，单位产量有正的剩余，厂商会增加产量，若P^*＜MC，单位产量有负的剩余，厂商会减少产量，直到P^*=MC为止，这时总剩余实现最大化。

垄断时，产量减少到q_m，垄断价格为P_m，消费者剩余为dP_mb，生产者剩余为P_mP^*cb，总剩余为dP^*cb。和竞争时相比，垄断造成了无谓损失，无谓损失的大小为bca的面积。

这部分无谓损失正好是因为减少的产量q_mq^*所造成的，在这部分产量上，P＞MC，单位产量是有剩余的，这部分剩余白白地损失了。

假设p(Q)=a-Q，MC恒为c。

在垄断时：MR=a-2Q

利润最大化时：MR=MC，a-2Q=c

得Q=(a-c)/2

P=a-Q=(a+c)/2

利润=Q(p-c)=(a-c)²/4。

在完全竞争时：MR=P=a-Q

利润最大化时：MR=MC，a-Q=c

得Q=a-c

p=c

利润为零。

垄断造成的福利损失为bca的面积，即(a-c)²/8。