问题
问答题
如图,A、B两球分别固定于轻质直角尺两端,直角尺可绕顶点O处的光滑固定转轴在竖直平面内自由转动。已知OA=OB=l,A球质量为m。当系统平衡时,OA与竖直方向的夹角为37°。(已知 )
)
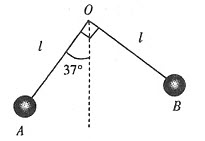
(1)求B球的质量mB;
(2)若将直角尺顺时针转动到OA位于水平处由静止释放,求释放瞬间A球的角加速度;
(3)当OA从水平位置由静止开始运动到竖直位置时,B球的速度为多少
(4)说明B球速度在什么位置最大。
答案
参考答案:
(1)由力矩平衡得
mglsin37°=mBglcos37°
B球的质量
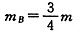
(2)转动惯量为J=(m+mB)l2= ml2
ml2
OA位于水平住置系统所受外力矩M=mgl
由转动定理,角加速度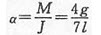
(3)释放后,由机械能守恒定律
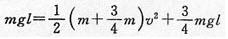
B球速度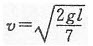
(4)当系统所受合外力矩为零时处于平衡位置,此时B球速度最大。
