问题
问答题
设随机变量Xi～
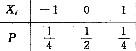(i=1，2)且满足P(X1X2=0)=1，求
(1)(X1，X2)的联合分布；
(2)P(X1=X2)；
(3)X1，X2是否相互独立．
答案
参考答案：[详解] (1)∵P(X1X2=0)=1，∴P(X1X2≠0)=0．
∴P(X1=1，X2=1)=P(X1=1，X2=-1)=P(X1=-1，X2=1)=P(X1=-1，X2=-1)=0．
∴立即可得表中阴影部分的数值
[*]
容易求出表中非阴影部分的数值．
(2)P(X1=X2)=P(X1=-1，X2=-1)+P(X1=0，X2=0)+P(X1=1，X2=1)=0．
(3)[*]
∴X1，X2不相互独立．
解析：
[分析]： 由P(X1X2=0)=1[*]P(X1X2≠0)=0．
[评注] 1°利用离散型二维联合分布表进行计算是常用的较简便的方法．
2°对于离散型二维随机变量：(i)[*]i，jpij=pi·．p·j[*]相互独立．
(ii)如果[*]i，j使pij≠pi·．p·j，则不相互独立．