问题
问答题
已知线性方程组
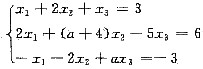有无穷多解，而A是三阶方阵，
，
，
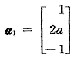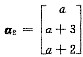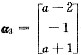分别是A关于特征值λ1=1，λ2=-1，λ3=0的三个特征向量．
(1)求A；
(2)计算行列式|2A3+E|．
答案
参考答案：[详解] (1)化增广矩阵为阶梯形[*]
由题设方程组有无穷多解，得a=-1或a=0．
当a=-1时，[*]线性相关，不可能为三个不同特征值的特征向量，不合题意．
当a=0时，[*]线性无关，符合题意．故a=0．
令[*]，则[*]
从而[*]
(2)∵P-1(2A3+E)P=2P-1A3P+P-1EP=2(P-1AP)3E
[*]
解析：
[分析]： 由已知线性方程组有无穷多解，可解出a的取值，但应使得α1，α2，α3线性无关(是三个不同特征值的特征向量)．在知道A的所有特征值、特征向量后，即可求出A及行列式|2A3+E|．
[评注] 求行列式|2A3+E|时，可直接代入A进行计算，但计算过程很复杂，而转化为相似对角形后，则可方便地得到结果．