问题
填空题
设函数f(x)在[0,1]上为连续函数,且
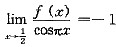 ,而
,而
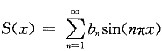 ,-∞<x<+∞,其中
,-∞<x<+∞,其中
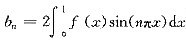 ,n=1,2,3,…,则
,n=1,2,3,…,则
 =______.
=______.
答案
参考答案:0
解析:
[分析]: 从S(x)的表达式可知,相当于将f(x)延拓为[-1,1]上的奇函数再展开为正弦级数,根据收敛定理求[*]即可.
[详解] 由S(x)的形式可知,这里对f(x)所作的是奇延拓,先将f(x)延拓为[-1,1)上的奇函数,再将f(x)延拓为整个实数轴上周期为2的周期函数,故
[*]
而 由[*]知f[*]从而有[*]
[评注] 若f(x)在[*]处不连续,则收敛于[*]
