已知A、B为三阶非零方阵,
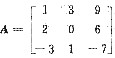 ,
,
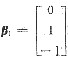 ,
,
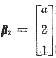 ,
,
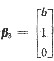 为齐次线性方程组Bx=0的三个解向量,且Ax=β3有非零解.
为齐次线性方程组Bx=0的三个解向量,且Ax=β3有非零解.
(1)求a,b的值;
(2)求Bx=0的通解.
参考答案:[详解] ①由β1,β2,β3均为Bx=0的解,而B≠O知,β1,β2,β3必线性相关,于是
[*]
由此解得a=3b.
又Ax=β3有非零解,即β3可由A的三个列向量
[*]线性表示,而α3=3α1+2α2,
可见β3可由α1,α2线性表示,因此β3,α1,α2线性相关,于是
[*]
解得b=5,从而a=15.故a=15,b=5.
②由题设r(B)≥1,于是3-r(B)≤2,而β1,β2为Bx=0的两个线性无关的解,故3-r(B)=2,可见β1,β2即可作为Bx=0的基础解系,故通解为x=k1β1+k2β2(k1,k2为任意常数).
解析:
[分析]: B≠O,β1,β2,β3为Bx=0的=三个解向量,于是必有行列式|[β1,β2,β3]|=0,再根据Ax=β3有解,即β3可由α1,α2,α3线性表示(这里易知α3=3α1+2α2),从而β3可由α1,α2线性表示,又得行列式|[β3,α1,α2]|=0.由此两个等式可解得a,b,或由r(A)=r(A[*]β3),可得b,再根据|[β1,β2,β3]|=0,又可解得a.
至于求Bx=0的通解,关键是确定B的秩.
[评注] 对于参数b,也可根据解的判定来确定.由Ax=β3有非零解,知r(A[*]β3)=r(A)≤2,
[*]
可见有b=5.
