问题
选择题
已知F1（-c，0），F2（c，0）分别是双曲线C1：
|
答案
解：如图所示，
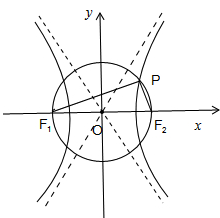
由题意可得∠F1PF2=90°，
又2∠PF1F2=∠PF2F1，
∴∠PF1F2=30°．
∴|PF2|=c，|PF1|=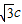 
．
由双曲线的定义可得：|PF1|-|PF2|=2a，
∴ 
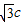?c=2a，
解得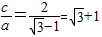
故选D．
搜题请搜索小程序“爱下问搜题”
已知F1（-c，0），F2（c，0）分别是双曲线C1：
|
解：如图所示，
由题意可得∠F1PF2=90°，
又2∠PF1F2=∠PF2F1，
∴∠PF1F2=30°．
∴|PF2|=c，|PF1|= ．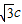
由双曲线的定义可得：|PF1|-|PF2|=2a，
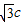∴ ?c=2a，
解得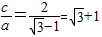
故选D．
