问题
问答题
求微分方程y"+y=f(x)满足初始条件y(0)=0,y’(0)=1的特解,其中连续函数f(x)满足条件
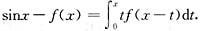
答案
参考答案:因为[*]于是题设条件可表为
[*]
两边对x求导,得
[*]
两边对x求导,整理可得
f"(x)+f(x)=-sinx,且f(0)=0,f’(0)=1
解上述方程组得[*]
可见原方程为
[*]
对应齐次方程通解为Y=C1cosx+C2 sinx,且特解可设为
y*=x(b1x+b2)cosx+x(b3x+b4)sinx
代入方程后得
[*]
再根据初始条件y(0)=0,y’(0)=1得所求解为
[*]
