问题
问答题
设u0=0,u1=1,un+1=aun+bun-1(n=1,2,…),其中a,b为常数,又设f(x)=
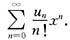
证明:f(x)=-eaxf(-x)。
答案
参考答案:令 g(x)=-eaxf(-x),
g’(x)=-aeaxf(-x)+eaxf’(-x),
g"(x)=-a2eaxf(-x)+2aeaxf’(-x)-eaxf"(-x),
故 g"(x)-ag’(x)-bg(x)=-eax[f"(-x)-af’(-x)-bf(-x)]=0
即g(x)满足微分方程①
又 g(0)=-f(0)=0,
g’(0)=-af(0)+f’(0)=1,
故g(x)也满足初始条件②,因此g(x)=f(x),
即 f(x)=-eaxf(-x)。
解析:
[分析]: 可令g(x)=-eaxf(-x),满足与f(x)相同的微分方程及初始条件,从而f(x)=g(x)。
[评注] 微分方程满足初始条件的解是唯一确定的,由无穷级数引出微分方程是一类重要题型。
