问题
问答题
已知实二次型f(x1，x2，x3)=xTAx的矩阵A满足
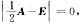且AB-3B=0，其中
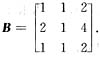
用正交变换x=Py化二次型为标准形，并写出所用正交变换及所得标准形；
答案
参考答案：由[*]|2E-A|=0，知矩阵A有特征值λ1=2，令B=(α1，α2，α3)，由AB-3B=0知B的每一列αj，满足Aαj-3αj=0，即Aαj=3αj，j=1，2，3。
显然B的第1，2列[*]线性无关，是属于A的特征值λ=3的线性无关特征向量，从而知A有二重特征值λ2=λ3=3。
设λ1=2对应的特征向量为[*]，则α1与α1，α2正交，于是有
[*]
解得 α3=[-1，0，1]T，将α1，α2正交化得：
[*]
再将正交向量组β1，β2，β3单位化得正交单位向量组：
[*]
令P=[η1，η2，η3]，则正交变换x=Py化二次型为标准形[*]