问题
问答题
设u0=0,u1=1,un+1=aun+bun-1(n=1,2,…),其中a,b为常数,又设f(x)=
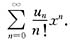
试导出f(x)满足的微分方程;
答案
参考答案:[*]
[*]
由 un+1=aun+bun-1,
得 f"(x)-af’(x)-bf(x)=0, ①
f(0)=u0=0,f’(0)=u1=1 ②
解析:
[分析]: 对f(x)逐项求导,再利用已知条件un+1=aun+bun-1,这里un相差二阶,可以预期要对f(x)求二阶导数,得关于f(x)的二阶微分方程;
