问题
问答题
如图所示,在粗糙的水平面上有一弹簧振子。已知物体的质量是m=1.0公斤,弹簧的弹性系数是k=100牛顿/米,摩擦系数μ=0.2。现把物体m从平衡位置拉伸0.07米后释放,振子由静止开始运动,运动方程的普遍形式可写为x=Acos(ω) t+φ0) +B。
确定振子释放后向左运动的运动方程。
答案
参考答案:
取物体未拉动时的位置为原点0,X轴正向向右。
在物体向左运动过程中,物体受到弹簧的拉力f1和摩擦力f2的作用,根据牛顿第二定律得到。代入表达式x=Acos(ωt+φ0) +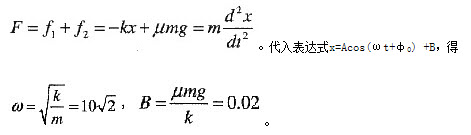 。
。
以释放时为时间起始点,当t=0时,v0=0,x0=△l,-Asinφ0=0可推出φ0=0。由B+Acosφ0=△l 可推出A=△l-B=0.07-0.02=0.05,所以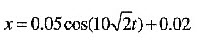 。
。
