问题
单项选择题
A是n阶矩阵，|A|=0的充分必要条件是： (1) Ax=0有非零解； (2) Ax=b有无穷多解； (3) A的列向量组中任何一个向量可被其余n-1个向量线性表出； (4) A的特征值全为0； (5) A的行向量组线性相关． 以上结论正确的是( )．
A．(1)(2)(3)(5)
B．(1)(2)(4)(5)
C．(1)(5)
D．(1)(2)(5)
答案
参考答案：C
解析：由已知得，
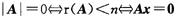有非零解．故(1)正确． 但r(A)＜n，不能保证r(A)=r(Ab)．故(2)不一定成立．相反，若Ax=b有无穷多解
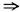r(A)=r(Ab)＜n．故(2)应排除． 由于矩阵的秩和其行向量组及列向量组的秩均相等，故
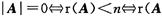的列向量组或行向量组)＜n
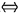A的列向量组(行向量组)线性相关．故(5)正确．但列向量组线性相关
存在某个向量可被其余n-1个向量线性表出．并不是每个向量均可被其余n-1个向量线性表出．故(3)应排除． 又
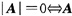有特征值0．但并不是A的n个特征值均为0．故(4)也应排除． 故应选C．