参考答案：

解析：计算基于无红利支付股票的欧式看跌期权的价格，其中执行价格为50美元，现价为50美元，有效期三个月，无风险年收益率为10%，年波动率为30%。若在两个月后预期支付红利为1.5美元，又如何计算
[解] 根据布莱克-斯科尔斯期权定价公式可知，
无收益资产欧式看跌期权定价公式为：
P=Xe^-r(T-t)N(-d₂)-SN(-d₁)，
其中：

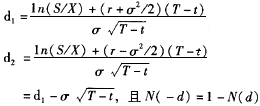
又根据题意可知：股票现价S=50，期权执行价格X=50，无风险利率r=10%，波动率σ=30%，有效期T-t=3个月=3/12=0.25。所以代入公式，可得：

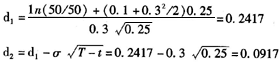
另外，通过标准正态分布表查表可得，N(d₁)=N(0.2417)=0.5955，N(d₂)=0.5366
所以，看跌期权价格：
p=Xe^-r(T-t)N(-d₂)-SN(-d₁)
=50e^-0.1×0.25(1-0.5366)-50(1-0.5955)=2.37
若在两个月后预期支付红利1.5美元，则应从现在股价中扣除两个月后预期支付红利的现值，折现时折现期限为2个月=2/12，即：标的资产股票不价格变为
S’=S-1.5e^-r(T-t)=50-1.5e^-0.1×(2/12)=48.52，此时再计算

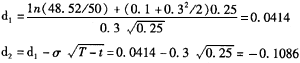
另外，通过标准正态分布表查表可得，N(d₁)=N(0.0414)=0.5165，
N(d₂)=0.5432，所以，若在两个月后预期支付红利1.5美元，则看跌期权价格变为：
p’=Xe^-r(T-t)N(-d₂)-S’N(-d₁)=50e^-0.1×0.250.5432-48.52(1-0.5165)=3.03