设有2个四元齐次线性方程组:
(Ⅰ)
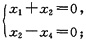 (Ⅱ)
(Ⅱ)
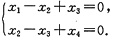
方程组(Ⅰ)和(Ⅱ)是否有非零公共解若有,求出所有的非零公共解;若没有,则说明理由.
参考答案:和(Ⅱ)的公共解,可以用下列几种方法求之.
法一 把(Ⅰ)、(Ⅱ)联立起来直接求解.设联立方程组的系数矩阵为A,用初等行变换将其化为含最高阶单位矩阵的矩阵,直接写出其基础解系(参阅本书试卷一第21题),从而求出所有的非零公共解.
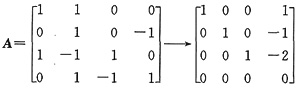
由于n-r(A)=4-3=1,基础解系是[-1,1,2,1]T,从而方程组(Ⅰ)、(Ⅱ)有公共解,且所有的非零公共解为
k[-1,1,2,1]T,k是任意非零实数.
法二 通过(Ⅰ)与(Ⅱ)各自的通解寻找公共解.为此,先求方程组(Ⅱ)的基础解系为
η1=[0,1,1,0]T,η2=[-1,-1,0,1]T.
下求方程组(Ⅰ)的基础解系.由
 知,其基础解系含2个解向量:
知,其基础解系含2个解向量:
ξ1=[0,0,1,0]T,ξ2=[-1,1,0,1]T.
那么k1ξ1+k2ξ2,l1η1+l2η2分别是(Ⅰ)、(Ⅱ)的通解,令其相等,则有
k1[0,0,1,0]T+k2[-1,1,0,1]T=l1[0,1,1,0]T+l2[-1,-1,0,1]T,
由此得[-k2,k2,k1,k2]T=[-l2,l1-l2,l1,l2]T.
比较两个向量对应分量得到k1=l1=2k2=2l2,所有非零公共解是
2k2[0,0,1,0]T+k2[-1,1,0,1]T=k2[-1,1,2,1]T,其中k2为非零任意常数.
法三 可以把一方程组的通解代入另一方程组寻找任意常数所满足的关系式,从而求出公共解.为方便计,将方程组(Ⅱ)的通解
c1η1+c2η2=[0,c1,c1,0]T+[-c2,-c2,0,c2]T
=[-c2,c1-c2,c1,c2]T
代入方程组(Ⅰ),得到
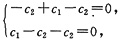 即c1=2c2.
即c1=2c2.
因而得到两方程组的非零公共解为
2c2η1+c2η2=c2(2η1+η2)=c2[[0,2,2,0]T+[-1,-1,0,1]T]
=c2(-1,1,2,1)T,c2为任意非零常数.
解析: 两个齐次线性方程组的公共解可用多种方法求得.
