问题
问答题
设f(x)在(0，+∞)内连续，f(1)=3，且
其中x，y∈(0，+∞)，求f(x)．
答案
参考答案：在等式两边依次对x，y求导，有
yf(xy)=
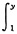f(t)dt+yf(x)，
xf(xy)=xf(y)+
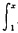f(t)dt． ①
在式①两边对x求导得到
f(xy)+xyf’(xy)=f(y)+f(x)． ②
取x=1，由式②得到
f(y)+yf’(y)=f(y)+3，
得f’(y)=
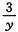，积分得
f(y)=3lny+C．
由f(1)=3，知C=3，所以
f(y)=3(lny+1)，
即f(x)=3(lnx+1)．
解析： 在所给等式两边分别对x，y求导．为去掉积分号需对x两次求导，再将f(1)=3代入化为f(y)所满足的一阶微分方程解之，求得f(y)，即f(x)．