问题
问答题
设A为三阶矩阵,有三个不同特征值λ1,λ2,λ3,对应的特征向量依次为α1,α2,α3,令β=α1+α2+α3.
β,Aβ,A2β线性无关
答案
参考答案:设k1β1+k2Aβ+k3A2β=0,
则
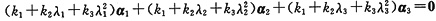
由α1,α2,α3线性无关,得因上方程组的系数矩阵的行列式为三阶范德蒙行列式,又因λ1≠λ2≠λ3,故该方程组所以β,Aβ,A2β线性无关.
解析: 用线性无关定义证明
设A为三阶矩阵,有三个不同特征值λ1,λ2,λ3,对应的特征向量依次为α1,α2,α3,令β=α1+α2+α3.
β,Aβ,A2β线性无关
参考答案:设k1β1+k2Aβ+k3A2β=0,
则
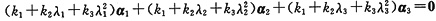
由α1,α2,α3线性无关,得因上方程组的系数矩阵的行列式为三阶范德蒙行列式,又因λ1≠λ2≠λ3,故该方程组所以β,Aβ,A2β线性无关.
解析: 用线性无关定义证明