问题
单项选择题
设随机变量X与Y相互独立，且均服从正态分布N(0，1)则______．
A．P(X+Y≥0)=1/4
B．P(X-Y≥0)=1/4
C．P(max(X，Y)≥0)=1/4
D．P(min(X，Y)≥0)=1/4
答案
参考答案：D
解析： 首先求出X+Y与X-Y的分布，如果X+Y～N(μ，σ2)，则P(X+Y≤μ)=1/2这个结论经常用到．求与max(X，Y)或min(X，Y)有关的概率常用下述事件分解法求之：
{max(X，Y)≥c}={X≥c}+{Y≥c}，
{min(X，Y)≤c}={X≤c}+{Y≤c}．
解一 记事件A={X≥0}，B={Y≥0}，则A与B相互独立，且
，
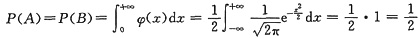故P(max(X，Y)≥0)=P({X≥0)∪{Y≥0})
=P(A∪B)=1-
=1-
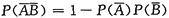
=1-
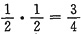
因X，Y独立，且X～N(0，1)，Y～N(0，1)，
故X+Y～N(0，2)， X-Y～N(0，2)，
于是P(X+Y≤0)=
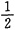，P(X-Y≤0)=
．
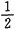因此P(X+Y≥0)=1-P(X+Y＜0)=1
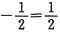，P(X-Y＞0)=
．
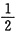因而A、B、C均不对，仅D入选．
解二 P(min(X，Y)≥0)=P({X≥0)∩{Y≥0})
=P(AB)=P(A)P(B)
=(1/2)(1/2)=1/4．
仅D入选．