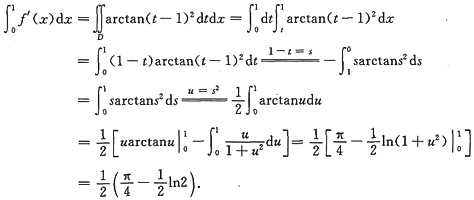问题
填空题
已知f’(x)=arctan(x-1)2,f(0)=0,则
 f(x)dx=______.
f(x)dx=______.
答案
参考答案:
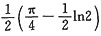
解析: 利用题设将f(x)化为变限积分,从而将所求定积分化为二重积分求之.
f(x)=f(x)-f(0)=
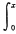 f’(t)dt
f’(t)dt
=
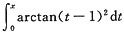
则
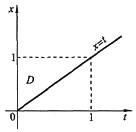
其中积分区域(见下图)

D={(t,x)|0≤t≤x,0≤x≤1}
交换上述二重积分的积分次序得到
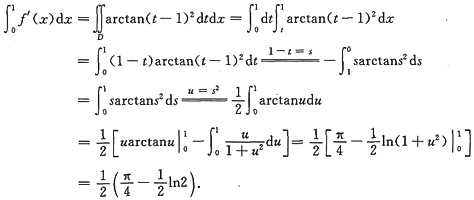
已知f’(x)=arctan(x-1)2,f(0)=0,则
 f(x)dx=______.
f(x)dx=______.
参考答案:
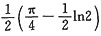
解析: 利用题设将f(x)化为变限积分,从而将所求定积分化为二重积分求之.
f(x)=f(x)-f(0)=
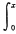 f’(t)dt
f’(t)dt
=
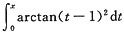
则

其中积分区域(见下图)

D={(t,x)|0≤t≤x,0≤x≤1}
交换上述二重积分的积分次序得到