∵a∈（0，1）∪（1，+∞），

当0＜x≤

1

2

时，函数y=4^x的图象如下图所示：

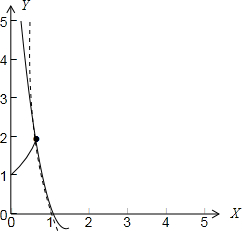
∵对任意的x∈(0，

1

2

]，总有4^x≤log_ax恒成立，若不等式4^x＜log_ax恒成立，则y=log_ax的图象恒在y=4^x的图象的上方（如图中虚线所示）

∵y=log_ax的图象与y=4^x的图象交于（

1

2

，2）点时，

a=

2

2

，

故虚线所示的y=log_ax的图象对应的底数a应满足

2

2

＜a＜1．

故答案为：（

2

2

，1）．