问题
问答题
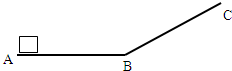
如图所示,在光滑水平面AB上,水平恒力F推动质量为1kg的物体从A点由静止开始作匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变,最高能到达C点,用速度传感器测量物体的瞬时速度,表中记录了部分测量数据,(g=10m/s2)求:
| t(s) | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | 2.6 | … |
| V(m/s) | 0.0 | 0.4 | 0.8 | … | 3.0 | 2.0 | 1.0 | … |
(2)斜面的倾角;
(3)t=2.1s时物体的速度.
答案
(1)(2)有表格可知,物块在水平面上做匀加速直线运动,在斜面上做匀减速直线运动.由a=
,可求得加速运动的加速度a1和减速运动的加速度a2.v-v0 t
a1=
m/s2=2m/s2; 0.4-0 0.2
a2=
m/s2=-5m/s2.2-3 0.2
由牛顿第二定律得:
F=ma1;
-mgsinθ=ma2;
求解得:F=2N;
θ=30°
(3)由表格可判断t=2.8s时速度减为0.设加速运动时间为t1,减速运动时间为t2,可列式:a1t1=a2t2;
t1+t2=2.8s,求解得:
t1=2s,t2=0.8s.
最大速度为:vmax=a1t1=4m/s
则2.1s时的速度为:
v=vmax+a2(t'-t1)=4-5×(2.1-2.0)m/s=3.5m/s
答:(1)恒力F的大小为2N;
(2)斜面的倾角30°;
(3)t=2.1s时物体的速度3.5m/s.
