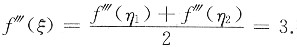问题
问答题
设函数f(x)在闭区间[-1,1]上具有三阶连续导数,且f(-1)=0,f(1)=1,f’(0)=0,证明:在开区间(-1,1)内至少存在一点ξ,使f"’(ξ)=3.
答案
参考答案:[证明] 由于f(x)三阶可导,可考虑泰勒公式,又f’(0)=0,应在x=0处展开
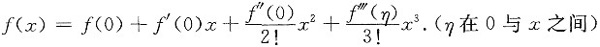
在上式中分别取x=1和x=-1,
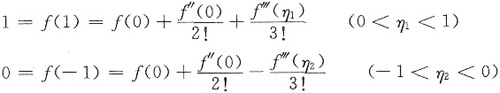
两式相减得
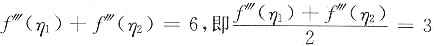
由于f"’(x)连续,则f"’(x)在闭区间[η2,η1]上有最大值M和最小值m.
则

由连续函数介值定理知,存在ξ∈[η2,η1]
 (-1,1),使
(-1,1),使