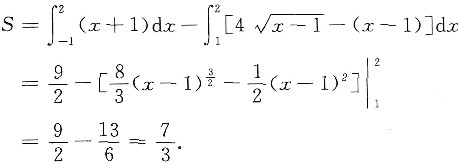问题
问答题
已知曲线L的方程为：
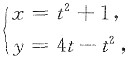(t≥0)．
(Ⅰ)讨论L的凹凸性；
(Ⅱ)过点(-1，0)引L的切线，求切点(x0，y0)，并写出切线的方程；
(Ⅲ)求此切线与L(对应于x≤x0的部分)及x轴所围成的平面图的面积．
答案
参考答案：
[分析]： 为确定L的凹凸性，须先求二阶导数
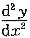并确定其正负，要解第(Ⅱ)问，首先要求出曲线上点(x0，y0)对应的参数t0处的斜率，然后求出切线方程，由(Ⅰ)和(Ⅱ)可知所求平面图形的基本形状，从而求出其面积．
[解法一] (Ⅰ)由于
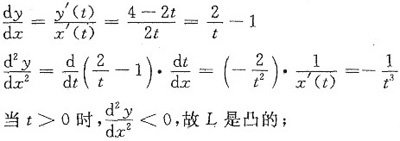
(Ⅱ)当t=0时，x’(0)=0，y’(0)=4，x(0)=1，y(0)=0，
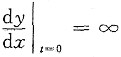
则t=0时，L在对应点处切线方程为x=1，不合题意，故设切点(x0，y0)对应的参数为t0＞0，则L在(x0，y0)处的切线方程为
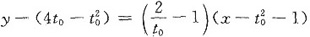
令x=1，y=0，得
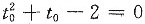
解得t0=1或t0=-2(舍去)
由t0=1知，切点为(2，3)，且切线方程为y=x+1．
(Ⅲ)令y=4t-t2=0，得t1=0，t2=4，对应曲线L与x轴的两个交点(1，0)和(17，0)，由以上讨论知曲线L和所求的切线如图所示，故所求平面图形的面积为
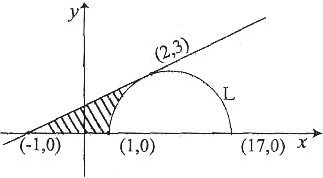
[解法二] (Ⅰ)同解法一．
(Ⅱ)由
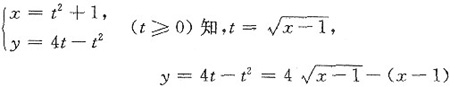
由于当x0=1时，L在对应点处切线方程为x=1，不合题意，故可设L在点(x0，y0)处的切线
方程为
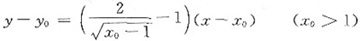
将x=1，y=0代入上式，得
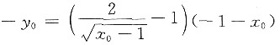
即
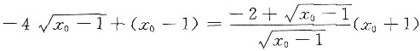整理得
解得x0=2，并得y0=3，因此切线方程为y=x+1．
(Ⅲ)在
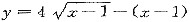中令y=0，得L与x轴的交点为(1，0)和(17，0)，故所求平面图形的面积为
