问题
问答题
设函数f(x)在[0，π]上连续，且
．
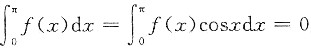试证明：在(0，π)内至少存在两个不同的点ξ1，ξ2，使f(ξ1)=f(ξ2)=0．
答案
参考答案：[证法一] 由
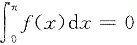及积分中值定理知，存在ξ∈(0，π)使f(ξ1)=0．
若在(0，π)内f(x)只有一个零点ξ1，则由
知，f(x)在(0，ξ1)与(ξ1，π)内异号．
不妨设在(0，ξ1)内f(x)＞0，在(ξ1，π)内f(x)＜0，又在(0，ξ1)内(cosx-cosξ1)＞0，在(ξ1，π)内(cosx-cosξ1)＜0，则
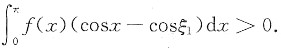
另一方面
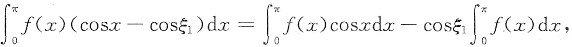
由
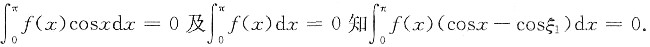
矛盾，原题得证．
[证法二] 令
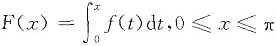，则有F(0)=0，F(π)=0
又
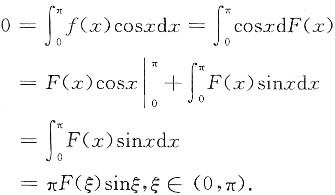
这里应用了积分中值定理，由于sinξ≠0，则F(ξ)=0，
由以上证明得0＜ξ＜π，F(0)=F(ξ)=F(π)=0，
对F(x)分别在区间[0，ξ]和[ξ，π]上用罗尔定理知，存在ξ1∈(0，ξ)和ξ2∈(ξ，π)，使
F’(ξ1)=F’(ξ2)=0，
即f(ξ1)=f(ξ2)=0．