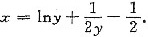问题
问答题
如图，C1和C2分别是
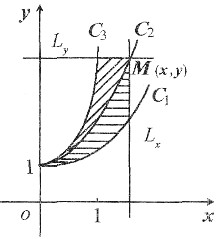
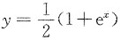和y=ex的图像，过点(0，1)的曲线C3是一单调增函数图像．过C2上任一点M(x，y)分别作垂直于x轴和y轴的直线Lx和Ly．记C1，C2与Lx所围图形的面积为S1(x)；C2，C3与Ly所围图形的面积为S2(y)．如果总有S1(x)=S2(y)，求曲线C3的方程x=φ(y)．
答案
参考答案：
[分析]： 先写出S1(x)和S2(y)的积分表达式，然后等式S1(x)=S2(y)两边对x求导，解出x=φ(y)．
[解] 由题设知
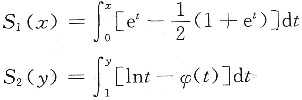
又S1(x)=S2(y)，则
即
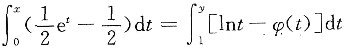
等式两端对x求导，得
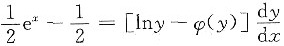
由y=ex得
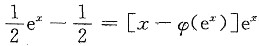
于是
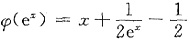
从而
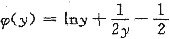
故曲线C3的方程为
