问题
问答题
设函数f(x)在区间[0，1]上连续，在(0，1)内可导，且f(0)=f(1)=0，
．试证
(1)存在
，使f(η)=η；
(2)对任意实数λ，必存在ξ∈(0，η)，使得
f’(ξ)-λ[f(ξ)-ξ]=1．
答案
参考答案：[证明] (1)要证f(η)=η，即要证f(η)-η=0，令F(x)=f(x)-x，由题设知F(x)在[0，1]上连续，又
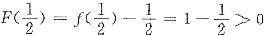，F(1)=f(1)-1=-1＜0，由连续函数零点定理知，存在
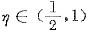，使F(η)=0即f(η)=η．
(2)为证存在ξ∈(0，η)，使得f’(ξ)-λ[f(ξ)-ξ]=1，也就只要证[f’(ξ)-1]-λ[f(ξ)-ξ]=0，令φ(x)=e-λx[f(x)-x]，则φ(x)在[0，η]上满足罗尔定理条件，由罗尔定理知存在ξ∈(0，η)，使φ’(ξ)=0．即e-λξ[(f’(ξ)-1)-λ(f(ξ)-ξ)]=0但e-λξ≠0，则[f’(ξ)-1]-λ[f(ξ)-ξ]=0，故f’(ξ)-λ[f(ξ)-ξ]=1．