问题
单项选择题
设F(x)是连续函数f(x)的一个原函数，“M
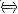N”表示M的充分必要条件是N，则必有
(A) F(x)是偶函数
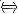f(x)是奇函数；
(B) F(x)是奇函数
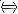f(x)是偶函数；
(C) F(x)是周期函数
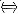f(x)是周期函数；
(D) F(x)是单调函数
f(x)是单调函数．
答案
参考答案：A
解析： 若F(x)是偶函数，由导函数的一个基本结论“可导的偶函数其导函数为奇函数”知，F’(x)=f(x)为奇函数，反之．
若f(x)为奇函数，则
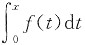为偶函数，f(x)的任一原函数F(x)可表示为
则F(x)是偶函数．
故应选(A)．
[分析二] 排除法：取f(x)=cosx+1，F(x)=sinx+x+1，显然f(x)连续，F’(x)=f(x)，且f(x)是偶函数，周期函数，但F(x)不是奇函数(F(0)≠0)，也不是周期函数，排除(B)和(C)选项．
若取f(x)=x，
，排除(D)，故应选(A)．
