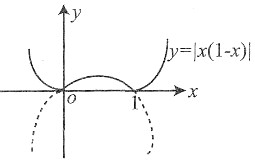
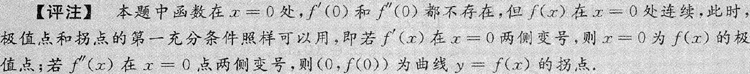问题
单项选择题
设f(x)=|x(1-x)|,则
(A) x=0是f(x)的极值点,但(0,0)不是曲线y=f(x)的拐点.
(B) x=0不是f(x)的极值点,但(0,0)是曲线y=f(x)的拐点.
(C) x=0是f(x)的极值点,且(0,0)是曲线y=f(x)的拐点.
(D) x=0不是f(x)的极值点,(0,0)也不是曲线y=f(x)的拐点.
答案
参考答案:C
解析: 由于f(x)=|x(1-x)|≥0,f(0)=0,则x=0为f(x)的极小值点,又
当x<0时,f(x)=-x(1-x)=x2-x,f"(x)=2>0
当x>0时,f(x)=x(1-x)=x-x2,f"(x)=-2<0
所以(0,0)是曲线y=f(x)的拐点.故应选(C).
[分析二] 曲线y=x(1-x)是过点(0,0)和(1,0)且开口向下的二次抛物线,而曲线y=|x(1-x)|是将x轴下方的图形对称翻向x轴上方(如图).
从图中不难看出x=0是f(x)的极小值点,(0,0)为曲线y=f(x)的拐点.