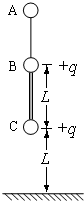
关于点电荷周围电势大小的公式为U=kQ/r,式中常量k>0,Q为点电荷所带的电量,r为电场中某点距点电荷的距离.如图所示,两个带电量均为+q的小球B、C,由一根长为L的绝缘细杆连接,并被一根轻质绝缘细线静止地悬挂在固定的小球A上,C球离地的竖直高度也为L.开始时小球A不带电,此时细线内的张力为T0;当小球A带Q1的电量时,细线内的张力减小为T1;当小球A带Q2的电量时,细线内的张力大于T0.
(1)分别指出小球A带Q1、Q2的电荷时电量的正负;
(2)求小球A分别带Q1、Q2的电荷时,两小球B、C整体受到小球A的库仑力F1与F2大小之比;
(3)当小球A带Q3的电量时细线恰好断裂,在此瞬间B、C两带电小球的加速度大小为a,求Q3;
(4)在小球A带Q3(视为已知)电量情况下,若B球最初离A球的距离为L,在细线断裂到C球着地的过程中,小球A的电场力对B、C两小球整体做功为多少?(设B、C两小球在运动过程中没有发生转动)
(1)对B、C整体分析,当小球A带Q1的电量时,细线内的张力减小为T1;
根据平衡条件得小球A带Q1电荷时电量为负,
当小球A带Q2的电量时,细线内的张力大于T0.根据平衡条件得小球A带Q2电荷时电量为正.
(2)根据库仑定律得
F1=
+kQ1q r 2B kQ1q r 2C
F2=
+kQ2q r 2B
,kQ2q r 2C
=F1 F2
. Q1 Q2
(3)细线断裂时(加速)
根据牛顿第二定律得:
GBC+F3=mBCa┅①,
球A不带电时(平衡)
根据平衡条件得:
GBC=T0┅②,
由①、②式,可得F3=
-T0┅③.T0a g
运用(2)的结论,得
=T0-T1 F3
┅④,Q1 Q3
再利用③、④式,得
Q3=
Q1. T0(a-g) (T0-T1)g
(4)小球A的电场力对B、C两小球整体做功等于各自做功的代数和.
W=WAB+WAC
WAB=(
-kQ3 L
)qkQ3 2L
WAC=(
-kQ3 2L
)q,kQ3 3L
W=
.2kQ3q 3L
答:(1)小球A带Q1电荷时电量为负,小球A带Q2电荷时电量为正;
(2)小球A分别带Q1、Q2的电荷时,两小球B、C整体受到小球A的库仑力F1与F2大小之比是
;Q1 Q2
(3)当小球A带Q3的电量时细线恰好断裂,在此瞬间B、C两带电小球的加速度大小为a,Q3是=
Q1. T0(a-g) (T0-T1)g
(4)在小球A带Q3(视为已知)电量情况下,若B球最初离A球的距离为L,在细线断裂到C球着地的过程中,小球A的电场力对B、C两小球整体做功为
.2kQ3q 3L
