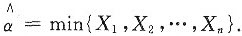问题
问答题
设随机变量X的分布函数为
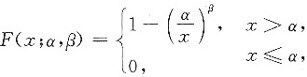
其中参数α＞0，β＞1．设X1，X2，…，Xn为来自总体X的简单随机样本，
(Ⅰ)当α=1时，求未知参数β的矩估计量；
(Ⅱ)当α=1时，求未知参数β的最大似然估计量；
(Ⅲ)当β=2时，求未知参数α的最大似然估计量．
答案
参考答案：
当α=1时，
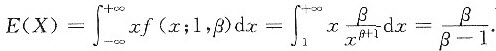
，所以当α=1时，参数β的矩估计量为
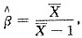
其中
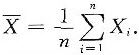
(Ⅱ)当α=1时，似然函数为
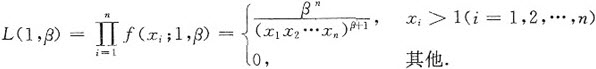
当xi＞1(i=1，2，…，n)时，L(1，β)＞0，取对数得
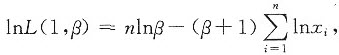
对β求导数，得
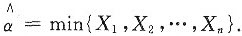
令
，β的最大似然估计量为
(Ⅲ)当β=2时，X的概率密度为
似然函数为
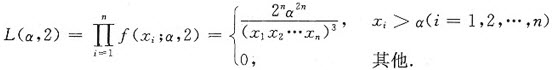
当xi＞α(i=1，2，…，n)时，α越大，L(α)越大，因而α的最大似然估计值为
，
α的最大似然估计量为