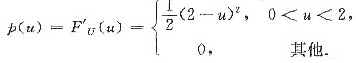问题
问答题
设随机变量X和Y的联合分布是正方形G=(z，y)|1≤x≤3，1≤y≤3上均匀分布，试求随机变量U=|X-Y|的概率密度p(u)．
答案
参考答案：
设U=|X-Y|的分布函数为FU(u)，则
FU(u)=P{U≤u)=P{|X-Y|≤u)．
当u≤0时，FU(u)=0，
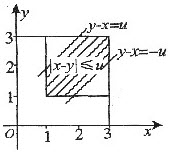
当0＜u＜2时，
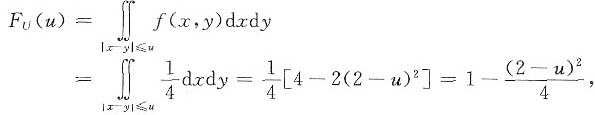
当u≥2时，FU(u)=1，
于是，
搜题请搜索小程序“爱下问搜题”
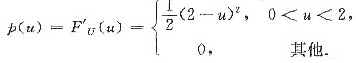
设随机变量X和Y的联合分布是正方形G=(z，y)|1≤x≤3，1≤y≤3上均匀分布，试求随机变量U=|X-Y|的概率密度p(u)．
参考答案：
设U=|X-Y|的分布函数为FU(u)，则
FU(u)=P{U≤u)=P{|X-Y|≤u)．
当u≤0时，FU(u)=0，
当0＜u＜2时，
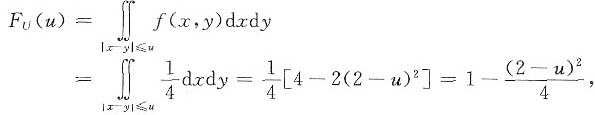
当u≥2时，FU(u)=1，
于是，