问题
问答题
假设0.50，1.25，0.80，2.00是来自总体X的简单随机样本值．已知Y=lnX服从正态分布N（μ，1）．
（1）求X的数学期望EX（记EX为b）；
（2）求μ的置信度为0.95的置信区间；
（3）利用上述结果求b的置信度为0.95的置信区间．
答案
参考答案：
Y=lnX，所以X=eY．题设条件Y为正态，故E(X)=E(eY)可用函数的期望的公式求得．
将X的样本可以转化成Y的样本，从而对正态Y～N(μ，1)中的μ求得置信区间．
最后，再从μ的置信区间转得b的置信区间．
(1)Y的概率密度为
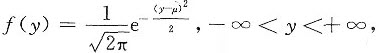
于是
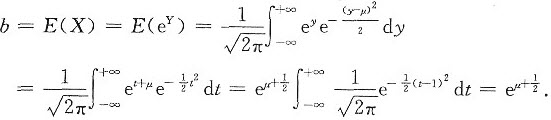
(2)当置信度1-α=0.95时，α=0.05．标准正态分布的双侧分位数等于1.96．故由
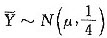，可得参数μ的置信度为0.95的置信区间为
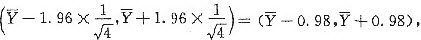
其中
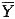表示总体Y的样本均值，
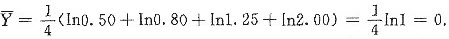
最后得到μ的置信度为0.95的置信区间(-0.98，0.98)．
(3)由指数函数ex的严格单调上升性，有
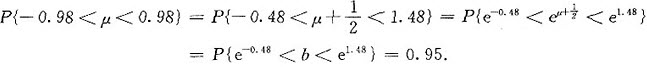
因此b的置信度为0.95的置信区间为(e-0.48，e1.48)．
