问题
问答题
设随机变量X与Y独立,其中X的概率分布为
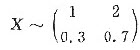 ,
,
而Y的概率密度为f(y),求随机变量U=X+Y的概率密度g(u).
答案
参考答案:
[简解] 设U的分布函数为G(u)和Y的分布函数为F(y)
G(u)=P{U≤u}=P{X+Y≤u}
=P{X=1}P{X+Y≤u|X=1}+P{X=2}P{X+Y≤u|X=2}
=0.3P{Y+1≤u|X=1}+0.7P{Y+2≤u|X=2}
=0.3P{Y+1≤u}+0.7P{Y+2≤u}
=0.3P{Y≤u-1}+0.7P{Y≤u-2}
=0.3F(u-1)+0.7F(u-2)
所以,g(u)=G’(u)=0.3F’(u-1)+0.7F’(u-2)=0.3f(u-1)+0.7f(u-2).
