问题
问答题
设u=f(x，y，z)有连续一阶偏导数，又函数y=y(x)及z=z(x)分别由下列两式确定：exy-xy=2．和
．
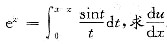答案
参考答案：[解] 等式exy-xy=2两端对x求导得
exy(y+xy’)-y-xy’=0
则[*]
等式[*]两端对x求导得
[*]
搜题请搜索小程序“爱下问搜题”
设u=f(x，y，z)有连续一阶偏导数，又函数y=y(x)及z=z(x)分别由下列两式确定：exy-xy=2．和
．
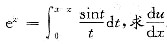参考答案：[解] 等式exy-xy=2两端对x求导得
exy(y+xy’)-y-xy’=0
则[*]
等式[*]两端对x求导得
[*]
