问题
问答题
已知函数z=f(x，y)的全微分dz=2xdx-2ydy，并且f(1，1)=2，求f(x，y)在椭圆域D=
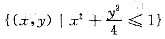上的最大值和最小值．
答案
参考答案：[解] dz=2xdx-2ydy=d(x2-y2)
则 z=x2-y2+C，
由f(1，1)=2知，C=2，f(x，y)=x2-y2+2
[*]
z=x2-y2+2=5x2-2 [-1，1]
显然x=0时取最小值-2，x=±1时取最大值3，故
fmax=f(1，0)=f(-1，0)=3，fmin=f(0，2)=f(0，-2)=-2