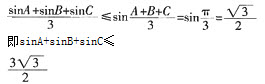问题
问答题
(1)叙述函数f(x)在区间[a,b]中上凸的定义,并证明f(x)=sinx在[0,π]中上凸
(2)若A、B、C为某三角形的三内角,证明sinA+sinB+sinC≤ 。
。
答案
参考答案:
(1)f(x)在区间[a,b]上的二阶导数f"(x)≤0,就说f(x)在区间[a,b]中上凸。
证明:f(x)=sinx,f"(x)=-sinx,f"(x)在区间[0,π]中小于等于0,故f(x)=sinx在[0,π]中上凸。
(2)证明:∵A、B、C为三角形三内角
∴A+B+C=π
又∵y=sinx(0<x<π)是凸函数
根据Jensen不等式:
∴