设A为三阶实对称矩阵,且存在可逆矩阵
 ,使得
,使得
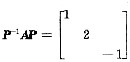 .又A的伴随矩阵A*有特征值λ0,λ0所对应的特征向量为
.又A的伴随矩阵A*有特征值λ0,λ0所对应的特征向量为
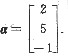
(1)求λ0的值;
(2)计算(A*)-1;
(3)计算行列式|A*+E|.
参考答案:[详解] (1)由题设,有[*],令P=[α1,α2,α3],其中[*][*],则Aα1=1·α1,Aα2=2·α2,Aα3=-1·α3,即α1,α2,α3分别是属于三个不同特征值λ1=1,λ2=2,λ3=-1的特征向量.而A为三阶实对称矩阵,其不同特征值对应的特征向量必正交,即
[*]
又A*α=λ0α,而α=-α3,于是有A*(-α3)=λ0(-α3),即A*α3=λ0α3,
从而AA*α3=λ0α3,|A|α3=λ0Aα3,可见[*]
因此有[*],故λ0=2.
(2)由Aα1=1·α1,Aα2=2·α2,Aα3=-1·α3,及[*]
有A[α1,α2,α3]=[α1,2α2,-α3],于是
A=[α1,2α2,-α3][α1,α2,α3]-1
[*]
故有 [*]
(3)由Aαi=λiαi,i=1,2,3,有[*],进而有[*]可见A*+E的特征值为[*],即μ1=-1,μ2=0,μ3=3,故|A*+E|=μ1μ2μ3=0.
解析:
[分析]: 本题关键条件是A为实对称矩阵,而[*],相当于已知A的三个特征值,且P的每列为对应特征向量,再根据不同特征值对应特征向量是正交的,可确定参数a,b.然后利用特征值与特征向量的定义可求出λ0.至于[*],只需求出A即可.而行列式|A*+E|利用特征值或相似矩阵均可计算.
[评注] 与A*有关的问题,一般均可考虑利用关系式AA*=A*A=|A|E进行化简.
