问题
问答题
某系统Q由两个子系统q1与q2联接组成,联接的方式有三种:1)q1,q2串联;2)q1,q2并联;3)q1与q2一个工作一个备用.已知子系统q1,q2的寿命X,Y均服从指数分布,其概率密度分别为
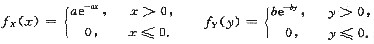
其中常数a>0,b>0,且a≠b.设系统Q的寿命为Z,分别求三种情况下,Q的寿命Z的概率密度.
答案
参考答案:[详解] (1)因q1,q2串联,其中一个损坏,系统便停止工作,所以Q的寿命Z=min(X,Y).因为
[*]
于是有 Fmin(z)=1-[1-FX(z)][1-FY(z)],
故 fmin(z)=fx(z)[1-FY(z)]+fY(z)[1-FX(z)]
[*]
(2)因q1,q2并联,当q1与q2均损坏时,系统才停止工作,所以Q的寿命Z=max(X,Y).
于是有 Fmax(Z)=FX(z)FY(z),
故 fmax(z)=fX(z)FY(z)+fY(z)FX(z)
[*]
(3)因为当q1损坏时,q2立即开始工作,当q2也损坏时,系统Q才停止工作.故Z=X+Y,于是
[*]
故 [*]
解析:
[分析]: 本题实质上为求随机变量函数的分布,q1,q2串联,意指寿命Z=min(X,Y);q1,q2并联,意指寿命Z=max(X,Y);而当q1损坏时,q2立即开始工作,意指Z=X+Y.
[评注] 对于常见二维随机变量函数的分布,如Z=min{X,Y},Z=max{X,Y),Z=X+Y等应作为公式加以记忆.
