问题
填空题
设X1，X2，X3，X4与Y1，Y2，Y3，Y4。分别是来自服从标准正态分布总体x和y的一组相互独立的简单随机样本，
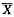和
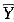分别为其样本均值，随机变量
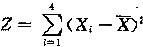
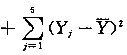，则数学期望=______．
答案
参考答案：G
解析：
[分析]： 从Z的构成形式可初步判断是服从χ2分布，须进一步确定其自由度，再利用χ2分布的性质确定其数学期望．
[详解] 由题设知，[*]
且[*]相互独立，于是有随机变量
[*]，根据χ2(n)的性质Eχ2(n)=n知，数学期望EZ=7．
[评注] χ2分布具有性质：
①设X～χ2(n1)，Y～χ2(n2)，并且X和Y相互独立，则X+Y～χ2(n1+n2)．
②若X～χ2(n)，则EX=n，DX=2n．