问题
问答题
计算
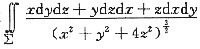，其中∑是球面(x-1)2+y2+z2=a2(n＞0，a≠1)，取外侧．
答案
参考答案：[详解] 令[*]，则
[*]
可见有[*]
(1)当a＜1时，∑：(x-1)2+y2+z2=a2，此时∑所围成的立体空间Ω不含坐标原点，
由高斯公式，有
[*]
(2)当a＞1时，令∑1：x2+y2+4z2=ε2，取内侧，ε＞0充分小．则
[*]
解析：
[分析]： 本题∑为封闭曲面，首先想到用高斯公式，但注意∑所围空间立体内是否包含“奇”点，即一阶偏导不连续的点，若是，应先挖掉奇点后再利用高斯公式．
[评注] 用一小的曲面挖掉奇点时，应注意使得在此小曲面上积分时比较容易．一般可考虑选择分母为常数的封闭曲面作为要求的小曲面．本题正是利用此思想，作小曲面：∑1：x2+y2+4z2=ε2，使得在此曲面上积分时，被积函数的分母为常数，从而便于用高斯公式计算出所要求的曲面积分．