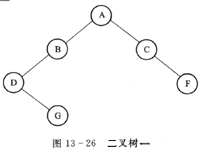
【说明】 一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左孩子分支向下查找，直到某个结点不存在左孩子时为止，该结点即为此二叉树的“最左下”结点。例如：图13-26所示的以A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。
二叉树的结点类型定义如下： typedef struct BSTNode{ int data； struct BSTNode * lch，* rch；//结点的左、右孩子指针 } * BSTree； 代码13-7中，函数BSTree Find_Del(BSTreeroot)的功能是：若root指向一棵二茶树的根结点，则找出该结点的右子树上的“最左下”结点*p，并从树中删除以*p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。 【代码13-7】 BSTree Find_Del(BSTree root) { BSTree p，pre； If(! root) / * root指向的二叉树为空树*/ return NULL； (1) ； / * 令p指向根结点的右子树*/ if( ! p) return NULL； (2) ； / * 设置pre的初值*/ while(p-＞lch) {/ * 查找“最左下”结点*/ pre＝p； p＝ (3) ； } if( (4) ＝＝root) / * root的右子树根为“最左下”结点*/ pre-＞rch＝NULL； else (5) ＝NULL；/ * 删除以“最左下”结点为根的子树*/ return p； }
参考答案：
解析：(1)p＝root-＞rch (2)pre＝root (3)p-＞lch (4)pre (5)pre-＞lch此题是一个关于二叉树操作的问题，首先来分析一下题目中对函数功能的描述。 BSTree Find_Del(BSTree root)功能是找出输入的二叉树的右子树上的“最左下”结点，删除以这个结点为根的子树并返回此结点的指针，如果二叉树的右子树不存在“最左下”结点，则返回空指针。 从(1)空所在的注释可知该空要填写的语句的功能是令指针p指向根结点的右子树，从二叉树的结点类型定义可知右孩子的指针为* rch，则第(1)空应该为：p＝root-＞rch。 接着看下面这段代码： if(!p) return NULL； (2) ； / * 设置pre的初值*/ while(p-＞lch){/ * 查找“最左下”结点*/ pre=p； p= (3) ； } 从注释可知这个循环的功能是查找二叉树根结点的右子树的“最左下”结点，从函数的返回指针为p可知，第(3)空的指针p应该总是指向左结点的，循环的目的是层层深入，而 pre指针则是p的前趋结点，在删除“最左下”结点时，pre将起到重要作用，所以第(2)空 pre指针的初值应该为二叉树的根结点：pre＝root，第(3)空应该为：p-＞lch。 从第(4)空后面的注释可知if语句是用来判断循环后所求的“最左下”结点是不是存在，如果存在则删除这个以“最左下”结点为根的树，从而得出空(4)和空(5)应该为：pre和 pre-＞lch。 综上所述，关注程序的注释是非常重要的，它对解题提供了许多有用的信息。