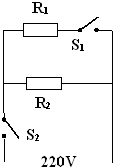
| 设函数f(x)=lnx-px+1,其中p为常数. (Ⅰ)求函数f(x)的极值点; (Ⅱ)当p>0时,若对任意的x>0,恒有在f(x)≤0,求p的取值范围; (Ⅲ)求证:
|
(Ⅰ)∵f(x)=lnx-px+1定义域为(0,+∞),
∴f′(x)=
-p=1 x
,1-px x
当p≤0时,f′(x)>0,f(x)在(0,+∞)上无极值点
当p>0时,令f'(x)=0,∴x=
∈(0,+∞),f'(x)、f(x)随x的变化情况如下表:1 p
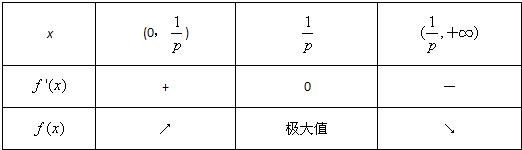
从上表可以看出:当p>0时,f(x)有唯一的极大值点x=1 p
(Ⅱ)当p>0时,在x=
处取得极大值f(1 p
)=ln1 p
,此极大值也是最大值,1 p
要使f(x)≤0恒成立,只需f(
)=ln1 p
≤0,1 p
∴p≥1
∴p的取值范围为[1,+∞)
(Ⅲ)令p=1,由(Ⅱ)知,lnx-x+1≤0,
∴lnx≤x-1,
∵n∈N,n≥2
∴lnn2≤n2-1,
∴
≤lnn2 n2
=1-n2-1 n2 1 n2
∴
+ln22 22
++ln32 32
≤(1-lnn2 n2
)+(1-1 22
)++(1-1 32
)=(n-1)-(1 n2
+1 22
++1 32
)<(n-1)-(1 n2
+1 2×3
++1 3×4
)=(n-1)-(1 n(n+1)
-1 2
+1 3
-1 3
++1 4
-1 n
)1 n+1
=(n-1)-(
-1 2
)=1 n+1 2n2-n-1 2(n+1)
∴结论成立